صفحه 1 از 1
مسائل حل نشده ریاضیات
ارسال شده: پنجشنبه ۳۰ مهر ۱۳۸۸, ۱:۲۰ ق.ظ
توسط misam5526
اعداد دوست :
عدد دوست در نظریه اعداد یک عدد طبیعی مثبت است که نسبت بین مقسوم علیههای آن عدد و خود عدد با یک یا چند عدد دیگر همانند است. دو عدد که در این خاصیت سهیم باشند یک زوج دوست نامیده میشوند. دستههای بزرگتر اعداد دوست نیز وجود دارد. عددی که چنین دوستانی نداشته باشد عدد تنها نامیده میشود.
خاصیت مورد نظر عبارت است از عدد غیر موهومی σ(n) / n است که در آن σ نشان دهنده تابع تقسیم کننده (مجموع تمام مقسوم علیهها) است. n یک عدد دوست است اگر n ≠ m باشد به طوری کهσ(m) / m = σ(n) / n .
اعداد ۱ تا ۵ همگی تنها هستند. کوچکترین عدد دوست ۶ است که زوج دوست (۲۸٬۶) که در ان ۶/(۶)σ مساویست با ۶ / (۶ + ۳ + ۲ + ۱) مساویست با ۲ همانطور که۲۸ / (۲۸)σ مساویست با ۲۸ / (۲۸ + ۱۴ + ۷ + ۴ + ۲ + ۱) مساویست با ۲. مقدار مشترک ۲ در این مورد یک عدد صحیح است اما در بسیاری از موارد چنین نیست.
مسائل حل نشده بسیاری در رابطه با اعداد دوست وجود دارد. بهرغم مشابهت نام، هیچ رابطه خاصی بین اعداد دوستانه یا اعداد اجتماعی وجود ندارد. هر چند تعریف این دو نیز شامل تابع تقسیم است.
تابع تقسیم
اگر n یک عدد مثبت طبیعی باشد (σ(n جمع مقسوم علیههای ان است . مثلا ۱۰ به ۵، ۲ ،۱ و ۱۰ بخش پذیر است و لذا σ(۱۰) = ۱ + ۲ + ۵ + ۱۰ = ۱۸
قرابت و دوستی
قرابت یا (K(n برای یک عدد مثبت طبیعی n به صورت عدد غیر موهومی σ(n)/n تعریف میشود مثلا κ(۱۰) = ۱۸/۱۰ = ۹/۵. کلمه قرابت و نشانه (K(n کاربردهای استاندارد نیستند و در اینجا فقط برای تسهیل بیان به کار رفتهاست. اعدادی که قرابت آنها مثل هم باشد دوست هستند مثلا K(۴۹۶) = K(۲۸) = K(۶)=۲ اعداد ۶، ۲۸ و ۴۹۶ همه کامل هستند و بنابراین دوست هستند به عنوان مثالی دیگر : (۳۰ و ۱۴۰) یک زوج دوستی هستند از آنجا که(K(۳۰) =K(۱۴۰ :

دوست بودن یک رابطه هم ارزی است و لذا شامل تقسیم اعداد صحیح به دستههایی از اعداد دوست هست .
اعداد تنها:
اعدادی که به یک دسته واحد تعلق دارند چون عدد دوست دیگری نیستند اعداد تنها هستند.
همه اعداد اول و توانهایشان کامل هستند، به طور عام تر هر جا اعداد n و(σ(n اول هستند به این معنا که بزرگترین مقسوم علیه مشترک آنها ۱ است به طوری که σ(n)/n یک تابع کاهش نا پذیر است عدد n تنهاست . برای یک عدد اول p داریم σ(p) = p + ۱ که مانند p عدد اول است .روشی عمومی برای این که بفهمیم یک عدد کامل است یا تنها وجود ندارد.
کوچکترین عددی که طبقه بندی آن معلوم نیست (تا سال ۲۰۰۷) ۱۰ است و حدس زده میشود که تنها باشد اگر نباشد کوچکترین دوست آن یک عدد نسبتا بزرگ خواهد بود.
دستههای بزرگ:
این مسئله باقی است که ایا دستههای بی نهایت بزرگ اعداد دوست وجود دارد؟ اعداد کامل یک دسته را تشکیل میدهند و حدس زده میشود که بی نهایت عدد کامل وجود دارد .(دست کم به اندازه تعداد اعداد اول مرسن) اما دلیلی برای ان نداریم . تا سال ۲۰۰۸ ،۴۴ عدد کامل شناخته شدهاست که بزرگترین انها ۱۹ میلیون رقم در سیستم ده دهی دارد . دستههای دیگری با اعداد شناخته شده بیشتر به خصوص آنهایی که از اعداد کامل چند گانه تشکیل میشوند که اعدادی هستند که قرابت آنها عدد صحیح است. تا اوایل سال ۲۰۰۸ دستهٔ اعداد دوست با قرابت مساوی ۹ ، ۲۰۷۹ عدد شناخته شده بودهاست گرچه میدانیم برخی از انها بسیار بزرگ هستند دستههای اعداد کامل چند جانبه (به استثنای خود اعداد کامل) حدس زده میشود که متناهی باشد.
Re: مسائل حل نشده ریاضیات
ارسال شده: پنجشنبه ۳۰ مهر ۱۳۸۸, ۱:۲۲ ق.ظ
توسط misam5526
اعداد فرما :
عدد فرما عدد صحیح و مثبتی است بصورت
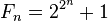
که در آن n عددی صحیح و غیر منفی است.
اگر چنین عددی اول هم باشد آنرا «عدد اول فرما» می نامند.
این اعداد را بنام پییر دو فرما نامگذاری کردهاند.
اگر 2m + 1 اول باشد، میتوان نشان داد m = 2n.
اثبات (با عکس نقیض): فرض کنید m توانی از 2 نباشد، بنابراين m دارای یک شمارنده فرد مانند 2k + 1 (بزرگتر از یک) است. بنابراین
m = (2k + 1)r
حال خواهیم داشت که 2m + 1 با استفاده از اتحاد دارای تجزیهٔ غیر بدیهی میشود. که این خلاف اول بودن این عدد است، پس این عدد به صورت
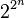
است. بنابراین هر عدد اولی که بصورت 2m + 1 باشد، عدد فرما است.
فرما که اغلب حدسهایش برای ریاضیدانان در خور توجه و قابل اعتماد بود مشاهده کرد که با گذاشتن چند عدد ۰ و ۱ و ۲ و ۳ و ۴ به جای n در فرمول بالا F اول است.
در سال ۱۷۳۲ اویلر نشان داد که (5)F مرکب است. تاکنون فقط به ازای n =0,...,۴ عدد اول فرما یافت شده است.
Re: مسائل حل نشده ریاضیات
ارسال شده: پنجشنبه ۳۰ مهر ۱۳۸۸, ۱:۲۴ ق.ظ
توسط misam5526
اعداد فوق کامل :
در ریاضیات یک عدد فوق کامل عددی صحیح مانند n است که در رابطهٔ زیر صدق کند

که در آن σ تابع تقسیم کننده میباشد.
اولین اعداد فوق کامل عبارتند از :2, 4, 16, 64, 4096, 65536, 262144
اگر n یک عدد فوق کامل زوج باشد باید به شکل توانی از 2 مانند 2k باشد به طوری که2k+1-1 یک عدد اول مرسن باشد.
مشخص نیست که عدد فوق کامل فردی وجود دارد یا نه. یک عدد فوق کامل فرد مانند n باید مربع کامل باشد به طوری هم n و هم (σ(n حداقل بر 3 عدد اول متمایز بخشپذیر باشند. هیچ عدد فوق کامل فردی کوچکتر از 7x1024 وجود ندارد.
اعداد کامل و فوق کامل زیر مجموعهای از دستهای بزرگتر از اعداد به نام (m,k)-کامل هستند که در رابطهٔ زیر صدق میکنند

Re: مسائل حل نشده ریاضیات
ارسال شده: پنجشنبه ۳۰ مهر ۱۳۸۸, ۱:۲۶ ق.ظ
توسط misam5526
تثلیث زاویه :
تثلیث زاویه از مسائل قدیمی و حل ناشده ریاضی است.
بزرگان ریاضی در طی دوران براحتی میتوانستند با کشیدن نیمساز، هر زاویه دلخواه را به دو بخش برابر قسمت کنند، ولی در سه قسمت کردن کمان عاجز بودند. بنابراین تثلیث یا سه بخش کردن زاویه یکی از مسائل عهد باستان گردید.
با آشنایی در حد مثلثات دبیرستانی میشود ثابت کرد این مسئله که جزء مسئلههای طرح شده در شاخه ساختمانهای هندسی است با کمک پرگار و ستاره (خطکش غیر مدرج) قابل حل نیست. ولی با حل یک معادله درجه ۳ ساده میتوانیم دریابیم که بینهایت زاویه وجود دارد که با کمک ستاره و پرگار قابل تثلیث است، از جمله زاویههای ۹۰ درجه یا ۴۵ درجه؛ و بینهایت زاویه وجود دارد که با کمک ستاره و پرگار قابل تثلیث نیست، از جمله زاویهٔ ۶۰ درجه. بنابراین، زاویهٔ ۶۰ درجه را نمیتوان، به کمک پرگار و خطکش، به سه بخش برابر تقسیم کرد.
تثلیث زاویه، به همراه تربیع دایره، تضعیف مکعب و چندضلعیهای منتظم محاط در دایره از مسائل سهگانه عهد باستان است طی قرنها حل نشده باقیمانده بود.
با وجود اثبات امکان ناپذیری حل این مسئله و مسئلههای مشابه با استفاده از ستاره و پرگار، عدهای تلاش میکنند این مسائل را حل کنند. در اصطلاح ریاضیکاران ایرانی، این عده نوابیغ نامیده میشوند. اگر چه زاویه دلخواه را نمیتوان با ابزارهای اقلیدسی دقیقا تثلیث نمود ولی ترسیمهایی با این ابزار وجود دارند که تثلیثهای بسیار خوبی را بدست میدهند مانند ترسیم حکّاک و نقّاش معروف آلبرشت دورر (Albercht Durer ) زاویه مفروض AOB را به عنوان یک زاویه مرکزی یک دایره در نظر بگیرید فرض کنید C آن نقطه تثلیث وتر AB باشد که به B نزدیکتر است در c عمود برAB را خارج می کنیم تا دایره را در D قطع کند به مرکز B و به شعاع BD قوسی رسم می کنیم را AB را در E قطع کند فرض کنید که F آن نقطه تثلیث EC باشد که به E نزدیک تر است دو باره به مرکز B به شعاع BF قوسی رسم می کنیم که دایره را در G قطع کند آنگاه OG یک خط تثلیث کننده تقریبی AOB است خطا در این روش با افزایش زاویه افزایش مییابد ولی برای زاویه 60 درجه حدود یک شستم زاویه (ثانیه ) است
Re: مسائل حل نشده ریاضیات
ارسال شده: پنجشنبه ۳۰ مهر ۱۳۸۸, ۱:۲۶ ق.ظ
توسط misam5526
تثلیث زاویه :
تثلیث زاویه از مسائل قدیمی و حل ناشده ریاضی است.
بزرگان ریاضی در طی دوران براحتی میتوانستند با کشیدن نیمساز، هر زاویه دلخواه را به دو بخش برابر قسمت کنند، ولی در سه قسمت کردن کمان عاجز بودند. بنابراین تثلیث یا سه بخش کردن زاویه یکی از مسائل عهد باستان گردید.
با آشنایی در حد مثلثات دبیرستانی میشود ثابت کرد این مسئله که جزء مسئلههای طرح شده در شاخه ساختمانهای هندسی است با کمک پرگار و ستاره (خطکش غیر مدرج) قابل حل نیست. ولی با حل یک معادله درجه ۳ ساده میتوانیم دریابیم که بینهایت زاویه وجود دارد که با کمک ستاره و پرگار قابل تثلیث است، از جمله زاویههای ۹۰ درجه یا ۴۵ درجه؛ و بینهایت زاویه وجود دارد که با کمک ستاره و پرگار قابل تثلیث نیست، از جمله زاویهٔ ۶۰ درجه. بنابراین، زاویهٔ ۶۰ درجه را نمیتوان، به کمک پرگار و خطکش، به سه بخش برابر تقسیم کرد.
تثلیث زاویه، به همراه تربیع دایره، تضعیف مکعب و چندضلعیهای منتظم محاط در دایره از مسائل سهگانه عهد باستان است طی قرنها حل نشده باقیمانده بود.
با وجود اثبات امکان ناپذیری حل این مسئله و مسئلههای مشابه با استفاده از ستاره و پرگار، عدهای تلاش میکنند این مسائل را حل کنند. در اصطلاح ریاضیکاران ایرانی، این عده نوابیغ نامیده میشوند. اگر چه زاویه دلخواه را نمیتوان با ابزارهای اقلیدسی دقیقا تثلیث نمود ولی ترسیمهایی با این ابزار وجود دارند که تثلیثهای بسیار خوبی را بدست میدهند مانند ترسیم حکّاک و نقّاش معروف آلبرشت دورر (Albercht Durer ) زاویه مفروض AOB را به عنوان یک زاویه مرکزی یک دایره در نظر بگیرید فرض کنید C آن نقطه تثلیث وتر AB باشد که به B نزدیکتر است در c عمود برAB را خارج می کنیم تا دایره را در D قطع کند به مرکز B و به شعاع BD قوسی رسم می کنیم را AB را در E قطع کند فرض کنید که F آن نقطه تثلیث EC باشد که به E نزدیک تر است دو باره به مرکز B به شعاع BF قوسی رسم می کنیم که دایره را در G قطع کند آنگاه OG یک خط تثلیث کننده تقریبی AOB است خطا در این روش با افزایش زاویه افزایش مییابد ولی برای زاویه 60 درجه حدود یک شستم زاویه (ثانیه ) است
Re: مسائل حل نشده ریاضیات
ارسال شده: پنجشنبه ۳۰ مهر ۱۳۸۸, ۱:۲۸ ق.ظ
توسط misam5526
تربیع دایره :
تربیع دایره یکی از مسائل قدیمی ریاضیات است. هدف آن رسم کردن مربعی است که مساحت آن برابر با مساحت دایرهای داده شده، فقط با استفاده از ستاره و پرگار، باشد.تلاش در حل این مساله که ناممکن بودن آن اثبات شده، یکی از عرصههای اصلی فعالیت نوابیغ است.
Re: مسائل حل نشده ریاضیات
ارسال شده: پنجشنبه ۳۰ مهر ۱۳۸۸, ۱:۳۰ ق.ظ
توسط misam5526
تضعیف مکعب :
تضعیف مکعب از مسائل باستانی ریاضیات است. یونانیان و قبل از آنها هندیان این مسئله را میشناختند. صورت مسئله این است:
«فقط با بهکار بردن ستاره و پرگار، مکعبی بسازید که حجم آن دوبرابر حجم مکعبی داده شده باشد.»
ثابت شده است که این مسئله جوابی ندارد[نیازمند منبع].
این مسئله به همراه تثلیث زاویه و تربیع دایره از مسائل مورد توجه نوابیغ بوده است.
Re: مسائل حل نشده ریاضیات
ارسال شده: پنجشنبه ۳۰ مهر ۱۳۸۸, ۱:۳۱ ق.ظ
توسط misam5526
حدس گلدباخ :
حدس گلدباخ در ریاضیات یکی از قدیمیترین مسائل حل نشده نظریه اعداد است. این حدس میگوید:
هر عدد زوج بزرگتر از ۲ را میتوان به صورت حاصلجمع دو عدد اول نوشت.
مثال: ۲۰=۱۷+۳ یا ۱۰=۷+۳ و ۴=۲+۲ و ۱۲=۷+۵.
این مسئله در حدود ۲۶۰ سال پیش توسط یک پزشک آلمانی علاقه مند به اثبات قضیههای ریاضی مطرح شد. شهود این پزشک متوجه حقیقت جالبی شده بود و آن هم این بود که هر عدد زوج را میتوان به صورت مجموع دو عدد اول نوشت. (البته عدد یک را به این خاطر از مجموعه اعداد اول کنار گذاشتند که صورت مسئلههای نظریه اعداد کوتاه تر شود. زیرا اگر این کار را نمیکردند بایستی در اکثر صورت مسئلههای مربوط به اعداد اول مینوشتند: «به غیر از یک») اکنون به دلیل همین موضوع عدد ۲ از حدس گلدباخ خارج شدهاست. گلدباخ هم عصر با اویلر بود. پس از تلاش فراوان و نا امید شدن از اثبات این حدس، گلدباخ از اویلر خواست تا مسئله را برایش حل کند. اویلر یکی از برجسته ترین شخصیتهای ریاضی آن زمان بود. نه اویلر و نه هیچیک از شاگردانش نتوانستند این مسئله را حل کنند. تا اینکه حدود ۶ سال پیش یک موسسه انتشاراتی در انگلستان به نام «تونی سیبر» برای کسی که بتواند این مسئله را حل کند مبلغ یک میلیون دلار جایزه تعیین کرد. این مسئله در عین سادگی صورت آن، هنوز حل نشده تا بتواند به عنوان قضیه مطرح شود.
این حدس توسط کامپیوترهای پیشرفته برای اعداد زوج بسیار بسیار بزرگی تست شده و جالب اینست که تا کنون هیچ مثال نقضی برای آن یافت نشدهاست.
گاهی اوقات فاصله شهود انسان تا لحظه اثبات یک مسئله آنقدر زیاد میشود که نسلها میآیند و میروند ولی همچنان حقیقت درباره مسئلهای مانند حدس گلد باخ نامشخص میماند.
شاید حل نشدن این مسئله به این خاطر باشد که با اعداد اول سر و کار دارد. زیرا خود مجموعه اعداد اول نیز ساختار جبری معینی ندارد.
در سال ۱۷۴۲ گلدباخ طی نامهای به اویلر مینویسد: ” به نظر میرسد که هر دو عدد زوج بزرگتر از ۲ را بتوان به صورت مجموع دو عدد اول نوشت.” این ادعای گلدباخ به حدس گلدباخ شهرت یافت و در این دو نیم قرن اخیر پایه و موضوع تحقیقات گستردهای شدهاست.هاردی ریاضیدان برجسته انگلیسی تصریح میکند که حدس گلدباخ یکی از دشوارترین مسائل حل نشده ریاضیات است.
حدس گلدباخ: هر عدد صحیح زوج بزرگتر از ۲ را میتوان به صورت مجموع دو عدد اول نوشت.
محاسبات عددی درستی این حدس را نشان میدهند که به طرق متعددی میتوان اعداد زوج را به صورت مجموع دو عدد اول نوشت. در سال ۱۹۷۳ چن نشان داد که اعداد زوج به اندازه کافی بزرگ را میتوان به صورت p+m نوشت که در آن p عددی اول و m عددی اول یا حاصل ضرب دو عدد اول است. گلدباخ حدس ضعیفتری زد که هر عدد فرد بزرگتر از ۷ را میتوان به صورت مجموع سه عدد اول نوشت.هر چند که این مساله هنوز باز است اما وینوگراف در سال ۱۹۳۷ نشان داد که برای همه اعداد فرد مثبت به اندازه کافی بزرگ این قضیه درست است ولی اندازه کافی را تعریف نکرد. شاگرد آن برودزین اثبات کرد که عدد ۳۱۴۳۴۸۹۰۷ به اندازه کافی بزرگ است (این عدد ۶۸۴۶۱۶۹ رقم دارد!). در سال ۲۰۰۲ دو ریاضی دان این عدد را به حدود
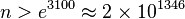
کاهش دادند. یعنی اگر برای اعداد کوچکتر از آن درستی قضیه چک شود، اثبات کامل میشود ولی این کار از عهده کامپیوترهای فعلی برنمی آید.
Re: مسائل حل نشده ریاضیات
ارسال شده: جمعه ۲۰ فروردین ۱۳۸۹, ۱:۵۸ ق.ظ
توسط misam5526
ای بابا اینا رو هم کسی نخونده که!!
بخونید ریاضی رو ....... امریکایی ها ریاضی خوندن تامکت ساختن!!


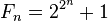
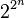 است. بنابراین هر عدد اولی که بصورت 2m + 1 باشد، عدد فرما است.
است. بنابراین هر عدد اولی که بصورت 2m + 1 باشد، عدد فرما است.

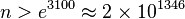 کاهش دادند. یعنی اگر برای اعداد کوچکتر از آن درستی قضیه چک شود، اثبات کامل میشود ولی این کار از عهده کامپیوترهای فعلی برنمی آید.
کاهش دادند. یعنی اگر برای اعداد کوچکتر از آن درستی قضیه چک شود، اثبات کامل میشود ولی این کار از عهده کامپیوترهای فعلی برنمی آید.