نگاه اجمالی
قوانینی که کمیتهای ماکروسکوپیک دخیل در فرآیندهای شامل گرما (مانند فشار ، حجم ، دما ، انرژی درونی و آنتروپی) را به هم مربوط میکنند، اساس علم ترمودینامیک را تشکیل میدهند. بیشتر کمیتهای ماکروسکوپیک (مثلا فشار ، حجم و دما) مستقیما به ادراک حسی ما مربوط میشوند. اگر بتوانیم کمیتهای ماکروسکوپیک را برحسب کمیتهای میکروسکوپیک تعریف کنیم، قادر خواهیم بود قوانین ترمودینامیک را بطور کمی به زبان مکانیک آماری بیان کنیم.
چشمانداز ترمودینامیک از نظر فیزیکدانان
چنانچه که گفته شد، اگر بتوانیم کمیتهای ماکروسکوپیکی را برحسب کمیتهای میکروسکوپیک تعریف کنیم، میتوانیم ترمودینامیک را بصورت ریاضی و فرمولبندی به زبان مکانیک آماری بیان کنیم. در واقع ، انجام چنین کاری گفته آر. سی. تولمان را تائید میکند که « توضیح علم ترمودینامیک به کمک علم انتزاعیتر مکانیک آماری ، یکی از بزرگترین دستاوردهای فیزیک است. » علاوه بر این ، بنیادیتر بودن نکات مکانیک آماری به ما امکان میدهد که اصول عادی ترمودینامیک را تا حد قابل توجهی تکمیل کنیم.
تصویر
توصیف میکروسکوپیکی
توصیف مشخصات کلی یک سیستم به کمک تعدادی از ویژگیهای قابل اندازه گیری آن (مانند فشار ، حجم ، دما ، انرژی داخلی ، آنتروپی ، چگالی و ...) ، که کم و بیش مستقیما با حواس ما قابل درک هستند، یک توصیف ماکروسکوپیکی است. این توصیفها نقطه شروع تمام بررسیها در تمام شاخههای فیزیک هستند. مثلا در بررسی مکانیک یک جسم صلب ، دیدگاه ماکروسکوپیکی را اتخاذ میکنیم.
مختصات مکانیکی
برای بررسی مکانیک یک سیستم صلب از دیدگاه ماکروسکوپیکی استفاده میکنیم، زیرا فقط جنبههای خارجی جسم صلب را در نظر میگیریم. مکان مرکز جرم نسبت به محورهای مختصات در یک زمان مشخص میشود. مکان و زمان و ترکیبی از آن دو مانند سرعت بعضی از کمیتهای ماکروسکوپیکی متداول در مکانیک را تشکیل میدهند و به مختصات مکانیکی مشهورند.
کاربرد مختصات مکانیک
مختصات مکانیکی برای تعیین انرژی پتانسیل و انرژی جنبشی جسم صلب نسبت به محورهای مختصات استفاده میشود، یعنی انرژی جنبشی و انرژی پتانسیل جسم به صورت یک کمیت کلی بکار میآیند. این دو نوع ، انرژی خارجی یا مکانیکی جسم صلب را تشکیل میدهند. هدف مکانیک ، تعیین روابط بین مختصات مکان و زمان است که با قوانین نیوتن سازگار باشند.
مختصات ترمودینامیکی
در ترمودینامیک توجهمان به داخل سیستم معطوف میشود. دیدگاه ماکروسکوپیکی را اختیار میکنیم و بر آن دسته از کمیتهای ماکروسکوپیکی تاکید میکنیم که رابطهای با حالت داخلی سیستم داشته باشند. تعیین کمیتهایی که برای توصیف این حالت داخلی لازم و کافی هستند، به عهده آزمایش است. آن کمیتهای ماکروسکوپیکی که به حالت داخلی سیستم مربوط هستند، مختصات ترمودینامیکی خوانده میشوند.
کاربرد مختصات ترمودینامیکی
مختصات ترمودینامیک برای تعیین انرژی داخلی سیستم بکار میآیند. هدف ترمودینامیک پیدا کردن روابط کلی بین این مختصات ترمودینامیکی است که با قوانین بنیادی ترمودینامیک سازگار باشند.
سیستم ترمودینامیکی و انواع آن
سیستمی که بتوان بر حسب مختصات ترمودینامیکی توصیف کرد، سیستم ترمودینامیکی میخوانند. در مهندسی ، سیستمهای مهم ترمودینامیکی عبارتند از: یک گاز ، مانند هوا ؛ یک بخار ، مانند آب ؛ یک مخلوط ، مانند بنزین و هوا و یک بخار در تماس با مایع خود ، مانند آمونیاک مایع و آمونیاک تبخیر شده. ترمودینامیک شیمیایی علاوه بر این سیستمها با جامدات ، فیلمهای سطحی و پیلهای الکتریکی سر و کار دارد. ترمودینامیک فیزیکی علاوه بر سیستمهای بالا شامل سیستمهایی نظیر سیستم تحت کشش ، خازن الکتریکی ، ترموکوپل و مواد مغناطیسی نیز میشود.
چشم انداز ترمودینامیک
مدیر انجمن: شوراي نظارت

-
- پست: 5234
- تاریخ عضویت: پنجشنبه ۲۵ خرداد ۱۳۸۵, ۲:۴۷ ب.ظ
- سپاسهای ارسالی: 1747 بار
- سپاسهای دریافتی: 4179 بار
- تماس:
چشم انداز ترمودینامیک
مرکز انجمنهای تخصصی گنجینه دانش
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]

-
- پست: 5234
- تاریخ عضویت: پنجشنبه ۲۵ خرداد ۱۳۸۵, ۲:۴۷ ب.ظ
- سپاسهای ارسالی: 1747 بار
- سپاسهای دریافتی: 4179 بار
- تماس:

قانون دوم ترمودینامیک و آنتروپی
قانون اول ترمودینامیک به معرفی انرژی درونی ، U ، منجر شد. این کمیت تابع حالتی است که بر مبنای آن ، مجاز بودن یک فرآیند مورد قضاوت قرار میگیرد و بیان میدارد که فقط تحولاتی مجاز است که انرژی داخلی کل سیستم منزوی ، ثابت بماند. قانونی که ملاک خودبخودی بودن را مشخص میسازد (قانون دوم ترمودینامیک) ، برحسب تابع حالت دیگری بیان میشود. این تابع حالت ، آنتروپی ، S ، است.
ملاحظه خواهیم کرد که بر مبنای آنتروپی قضاوت میکنیم که آیا یک حالت بطور خودبخودی از حالت دیگری قابل حصول میباشد. در قانون اول با استفاده از انرژی داخلی ، تحولات مجاز مشخص میشود (آنهایی که انرژی ثابت دارند). از قانون دوم با استفاده از آنتروپی ، تحولات خودبخودی از بین همان فرآیندهایی مشخص میشود که بر مبنای قانون اول مجاز میباشد.
بیان قانون دوم
آنتروپی سیستم منزوی در یک فرآیند خودبخودی افزایش مییابد
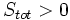
که
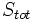 ، آنتروپی تمام قسمتهای سیستم منزوی میباشد.
، آنتروپی تمام قسمتهای سیستم منزوی میباشد.
از آنجایی که فرآیندهای برگشت ناپذیر (مانند سرد شدن شیئی تا دمای محیط و انبساط آزاد گازها) خودبخودی است، در نتیجه همه آنها با افزایش آنتروپی توام میباشند. این نکته را میتوان به این صورت مطرح کرد که در فرایندهای برگشت ناپذیر آنتروپی تولید میشود. از طرف دیگر ، در فرایند برگشت پذیر توازن وجود دارد، یعنی سیستم با محیط در هر مرحله در تعادل است. هر مرحله بسیار کوچک در این مسیر برگشت پذیر بوده و پخش نامنظم انرژی روی نمیدهد و در نتیجه آنتروپی افزایش نمییابد، یعنی در فرآیند برگشت پذیر آنتروپی ایجاد نمیشود. آنتروپی در فرآیندهای برگشت پذیر از بخشی از سیستم منزوی به بخش دیگری منتقل میگردد.
تعریف آماری آنتروپی
بر مبنای تعریف آماری ، فرض میشود که در واقع میتوانیم با استفاده از فرمول ارائه شده توسط لوودیگ بولتزمن (Ludwing Boltzmann) در سال 1896 ، آنتروپی را محاسبه کنیم:
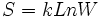
که k، ثابت بولتزمن است:
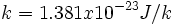
این ثابت به صورت
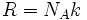
به ثابت گاز ربط دارد. کمیت W تعداد راههای متفاوتی است که سیستم میتواند با توزیع اتمها یا مولکولها بر روی حالتهای در دسترس به انرژی خاصی برسد. واحد آنتروپی با واحد k یکسان است. در نتیجه واحد آنتروپی مولی ،
 میباشد؛ (این با واحد R و ظرفیت گرمایی یکی است.)
میباشد؛ (این با واحد R و ظرفیت گرمایی یکی است.)
آخرین ويرايش توسط 1 on ganjineh, ويرايش شده در 0.
مرکز انجمنهای تخصصی گنجینه دانش
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]

-
- پست: 5234
- تاریخ عضویت: پنجشنبه ۲۵ خرداد ۱۳۸۵, ۲:۴۷ ب.ظ
- سپاسهای ارسالی: 1747 بار
- سپاسهای دریافتی: 4179 بار
- تماس:
تعریف ترمودینامیکی انرژی
در روش ترمودینامیکی ، تمرکز بر روی تغییر آنتروپی در طول یک فرایند ، dS ، میباشد، نه مقدار معلق S. تعریف dS بر این مبناست که میتوان میزان پخش انرژی را به انرژی مبادله شده به صورت گرما ، در حین انجام فرایند ربط داد. تعاریف آماری و ترمودینامیکی با هم سازگار میباشند. در شیمی فیزیک این یک لحظه نشاط آور است که بین خواص تودهای (که مورد نظر ترمودینامیک است) و خواص اتمها یک ارتباط برقرار شود.

در روش ترمودینامیکی ، تمرکز بر روی تغییر آنتروپی در طول یک فرایند ، dS ، میباشد، نه مقدار معلق S. تعریف dS بر این مبناست که میتوان میزان پخش انرژی را به انرژی مبادله شده به صورت گرما ، در حین انجام فرایند ربط داد. تعاریف آماری و ترمودینامیکی با هم سازگار میباشند. در شیمی فیزیک این یک لحظه نشاط آور است که بین خواص تودهای (که مورد نظر ترمودینامیک است) و خواص اتمها یک ارتباط برقرار شود.

مرکز انجمنهای تخصصی گنجینه دانش
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]

-
- پست: 5234
- تاریخ عضویت: پنجشنبه ۲۵ خرداد ۱۳۸۵, ۲:۴۷ ب.ظ
- سپاسهای ارسالی: 1747 بار
- سپاسهای دریافتی: 4179 بار
- تماس:
تغییر آنتروپی محیط
تغییر آنتروپی محیط را با علامت 'dS نشان میدهیم. علامت پریم مربوط به محیط سیستم واقعی که در سیستم منزوی بزرگ قرار دارد، مربوط میشود. محیط را با یک مخزن حرارتی بزرگ (عملا یک حمام آب) نشان میدهیم که در دمای T باقی میماند. مقدار گرمای منتقل شده به مخزن در اثر انجام کار مانند سقوط یک وزنه را با 'dq نشان میدهیم که این گرما به مخزن منتقل میشود. هرچه مقدار گرمای بیشتری به مخزن منتقل شود، حرکت حرارتی بیشتری هم در آن ایجاد میشود و از این رو ، پخش انرژی به میزان بیشتری اتفاق میافتد. از این نکته استنباط میشود که:

اگر گرما به مخزن سردی منتقل شود، کیفیت انرژی نسبت به موردی که آن گرما به مخزن گرمتری داده شود، انحطاط بیشتری خواهد داشت. در مورد اخیر میتوانیم در اثر جاری شدن گرمای 'dq از یک مخزن سرد به مخزن سردتری کار استخراج کنیم، اما اگر این گرما مستقما به مخزن سردتر منتقل شود، استخراج چنین کاری امکان پذیر نیست.
نتیجه میگیریم که اگر مقدار معین انرژی به صورت گرما به مخزن گرمی داده شود، آنتروپی کمتری ایجاد میشود تا اینکه آن انرژی به مخزن سردی داده شود. سادهترین راهی که میتوان این وابستگی دمایی را به حساب آورد، چنین است: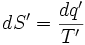
که 'T دمایی است که در آن دما ، انتقال گرما صورت گرفته است. برای یک تغییر قابل اندازه گیری در دمای ثابت چنین داریم:
وقتی که مقدار زیادی حرکت حرارتی در دمای پایین ایجاد شود، تغییر آنتروپی بزرگی اتفاق میافتد. برای فرآیند آدیاباتیک:
0 = 'q وقتی 0 = 'S∆
این نتیجه برای هر فرآیندی ، برگشت پذیر یا برگشت ناپذیر ، صحیح است، تا زمانی که مناطق گرم محلی در محیط ایجاد نشود، یعنی زمانی این نتیجه صحیح است که محیط ، تعادل درونی خود را حفظ کند. اگر مناطقی محلی بوجود آید، انرژی از این مناطق بطور خودبخودی پخش میشود و در نتیجه آن آنتروپی تولید میشود. موقعی که یک واکنش شیمیایی با تغییر آنتالپی H∆ در سیستمی انجام میشود، گرمایی که در فشار ثابت وارد محیط میشود، برابر با . بنابراین تغییر آنتروپی محیط برابر است با:

تغییر آنتروپی محیط را با علامت 'dS نشان میدهیم. علامت پریم مربوط به محیط سیستم واقعی که در سیستم منزوی بزرگ قرار دارد، مربوط میشود. محیط را با یک مخزن حرارتی بزرگ (عملا یک حمام آب) نشان میدهیم که در دمای T باقی میماند. مقدار گرمای منتقل شده به مخزن در اثر انجام کار مانند سقوط یک وزنه را با 'dq نشان میدهیم که این گرما به مخزن منتقل میشود. هرچه مقدار گرمای بیشتری به مخزن منتقل شود، حرکت حرارتی بیشتری هم در آن ایجاد میشود و از این رو ، پخش انرژی به میزان بیشتری اتفاق میافتد. از این نکته استنباط میشود که:

اگر گرما به مخزن سردی منتقل شود، کیفیت انرژی نسبت به موردی که آن گرما به مخزن گرمتری داده شود، انحطاط بیشتری خواهد داشت. در مورد اخیر میتوانیم در اثر جاری شدن گرمای 'dq از یک مخزن سرد به مخزن سردتری کار استخراج کنیم، اما اگر این گرما مستقما به مخزن سردتر منتقل شود، استخراج چنین کاری امکان پذیر نیست.
نتیجه میگیریم که اگر مقدار معین انرژی به صورت گرما به مخزن گرمی داده شود، آنتروپی کمتری ایجاد میشود تا اینکه آن انرژی به مخزن سردی داده شود. سادهترین راهی که میتوان این وابستگی دمایی را به حساب آورد، چنین است:
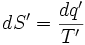
که 'T دمایی است که در آن دما ، انتقال گرما صورت گرفته است. برای یک تغییر قابل اندازه گیری در دمای ثابت چنین داریم:

وقتی که مقدار زیادی حرکت حرارتی در دمای پایین ایجاد شود، تغییر آنتروپی بزرگی اتفاق میافتد. برای فرآیند آدیاباتیک:
0 = 'q وقتی 0 = 'S∆
این نتیجه برای هر فرآیندی ، برگشت پذیر یا برگشت ناپذیر ، صحیح است، تا زمانی که مناطق گرم محلی در محیط ایجاد نشود، یعنی زمانی این نتیجه صحیح است که محیط ، تعادل درونی خود را حفظ کند. اگر مناطقی محلی بوجود آید، انرژی از این مناطق بطور خودبخودی پخش میشود و در نتیجه آن آنتروپی تولید میشود. موقعی که یک واکنش شیمیایی با تغییر آنتالپی H∆ در سیستمی انجام میشود، گرمایی که در فشار ثابت وارد محیط میشود، برابر با . بنابراین تغییر آنتروپی محیط برابر است با:

مرکز انجمنهای تخصصی گنجینه دانش
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]

-
- پست: 5234
- تاریخ عضویت: پنجشنبه ۲۵ خرداد ۱۳۸۵, ۲:۴۷ ب.ظ
- سپاسهای ارسالی: 1747 بار
- سپاسهای دریافتی: 4179 بار
- تماس:
انرژی درونی
مجموع انرژیهای جنبشی و پتانسیل کلیه ذرههای یک جسم را انرژی درونی یا داخلی آن جسم مینامند.
نگاه اجمالی
اگر دستهای خود را به هم بمالید، مشاهده میکنید که دستهای شما گرم تر شده است. در این حالت انرژی جنبشی دستها کجا رفته است؟ چون دستها گرم تر شدهاند، میتوان نتیجه گرفت که انرژی درونی آنها افزایش یافته است. در نتیجه میتوان گفت که در اثر مالش انرژی جنبشی دستها به انرژی درونی آنها تبدیل شده است.
انرژی داخلی V و آنتروپی S ، دو تابع اساسی ، برای توصیف سیستمهای ترمودینامیکی در حالت تعادلاند، هر سیستم ماکروسکوپیکی که متشکل از انبوه اتم و مولکولهاست، از قانون بقای انرژی تبعیت میکند. حرکت بزرگ مقیاس سیستم از قانون بقای انرژی مکانیکی تبعیت میکند و در غیاب میدانهای الکترومغناطیسی ، انرژی باقی مانده در سیستمی که منزوی است پایسته میماند، این کمیت همان انرژی داخلی است.
سیر تحولی و رشد
از لحاظ تاریخی ، تشخیص اینکه کمیتی پایسته بصورت تابع تومودینامیکی انرژی (یعنی تابعی که از قانون پایستگی تبعیت میکند) وجود دارد، پیش از ظهور دیدگاه اتمی ماده حاصل شد. پس این مفهوم میبایستی منحصرا از طریق تجربیات ماکروسکوپیکی شکل گرفته باشد. آزمایشها و حدسیات اولیه بنجامین تامسون (کنت رامفورد) درباره ماهیت گرما او را به این نتیجه رساند که گرما نوعی حرکت است. کارهای تجربی بعدی جیمز پرسکارت ذول در تعیین معادل مکانیکی گرما و نظریه پرفلزی ویلیام تامسون (لرد کلوین) بطور قطع نشان دادند که انرژی سیستم ماکروسکوپیکی منزوی با به حساب آوردن گرما پایسته است. این همان قانون اول ترمودینامیک است و تابع پایسته نیز انرژی داخلی است.
مفهوم انرژی داخلی یا درونی
بنابر نظریه جنبشی مولکولی ، هر ماده از ذرات ریزی تشکیل شده است که با سرعتها و در نتیجه انرژیهای متفاوت در حرکت و جنبش هستند. علاوه بر این مانند مدل ارتعاش یک جسم جامد ، ذرههای جسم دارای انرژی پتانسیل نیز هستند. این انرژی به فنری که در مدل ارتعاشی اتمها را به هم متصل میکرد، مربوط است. مجموع انرژیهای جنبشی همه اتمها و مولکولهای تشکیل دهنده جسم یا دستگاه و انرژی پتانسیل مربوط به برهمکنشهای آنها ، بدون انرژیهای جنبشی و پتانسیل جسم یا دستگاه نسبت به بیرون خود یا انرژیهای هسته درون اتمهای آن.
ارتباط انرژی درونی با دما
انرژی درونی چای یک فنجان که مدتی مانده و سرد شده است، کمتر از وقتی است که چای داغ بوده است. چای یخ کرده دمای پایین تری دارد و چای داغ دمایش بالاتر است. به این ترتیب هر چه دمای جسمی بالاتر باشد، انرژی درونی آن بیشتر است. یعنی ذرههای آن دارای انرژی جنبشی و پتانسیل بیشتری هستند.
ارتباط انرژی جنبشی با دما
اگر انرژی جنبشی ذرات یک جسم را بر تعداد ذرات تشکیل دهنده جسم تقسیم کنیم، انرژی جنبشی متوسط یک ذره بدست میآید. انرژی جنبشی متوسط ذرات چای داغ که دمای بالاتری دارد، بیشتر از انرژی جنبشی متوسط ذرههای چای سرد شده است که دمای پایین تری دارد. لذا نتیجه میگیریم که دمای جسم با انرژی جنبشی متوسط ذرههای تشکیل دهنده آن متناسب است.
این امر در ابعاد اتمی یا ابعاد میکروسکوپی بسیار مهم و مورد توجه است. به عنوان مثال در مباحث ترمودینامیک و مکانیک آماری با استفاده از روابط خاصی این انرژی در موارد مختلف محاسبه شده و با توجه به به مقدار آن در مورد وضعیت سیستم بحث می گردد. بنابر این میتوان گفت که هر چه دمای جسم بالاتر رود ، انرژی جنبشی متوسط ذرههای آن نیز افزایش خواهد یافت.
انرژی جنبشی متوسط ذرههای دو جسم متفاوت که دمای یکسانی دارند، با هم برابر است. به عنوان یک مورد ملموس و قابل مشاهده میتوان به این مورد اشاره کرد که انرژی جنبشی متوسط ذرههای آبی که بوسیله یک لیوان از استخری برداشته شده است، با انرژی جنبشی متوسط ذرههای آب استخر برابر است. ولی به دلیل تفاوت تعداد ذرههای آب لیوان و آب استخر، انرژی جنبشی و در نتیجه انرژی درونی یکسانی ندارند. بلکه انرژی درونی آب لیوان به مراتب کمتر از انرژی درونی آب استخر است.
اختلاف انرژی داخلی
بطور مفهومی ، تفاوت انرژی داخلی بین دو حالت را میتوان به صورت کار مکانیکی انجام شدهای در نظر گرفت که سیستمی بی دررو (یعنی سیستمی با انزوای گرمایی) را از حالت (A) به حالت نهایی (B) میبرد. اگر نتوان فرآیندی بی دررو A → B یافت (یعنی اگر فرآیند برگشت ناپذیر باشد)، فرآیند B → A وجود دارد. بنابراین به روش مکانیکی میتوان تفاوت انرژی داخلی بین دو حالت را اندازه گیری کرده مشروط بر آنکه ماده از سیستم خارج یا به آن وارد نشود. طبیعتا فقط تفاوت انرژی داخلی است که کمیت در خور توجهی است و مقدار مطلق انرژی داخلی به خودی خود دارای معنی فیزیکی نیست.
بیان ریاضی انرژی داخلی
هر افزایش جزئی انرژی داخلی سیستم ، du برابر است با مجموع کار انجام شده روی سیستم đw و گرمای وارد شده đφ ، به سیستم (یعنی قانون اول ترمودینامیک) که به صورت du = đw + đφ نشان داده میشود. در این جا خط تیره کوچکی که روی نماد دیفرانسیل d که شکل đ وجود دارد، دیفرانسیل غیرحقیقی را نشان میدهد. ضرورت این انحرافات ریاضیاتی ، برای نشان دادن این واقعیت است که w و φ تابعهای حالت نیستند.
به عبارت دیگر ، کمیت گرما و کار جذب شده در سیستم بستگی به سیری دارد که سیستم میپیماید تا از حالت اولیه به حالت کنونیاش (یعنی حالت نهایی) برسد. در اکثر موارد حالت سیستمهای تک مؤلفهای مانند گاز را میتوان با دستگاه مختصاتی دکارتی نشان داد که در آن یکی از محورها فشار P و دیگری حجم V را نشان میدهد. در نتیجه میتوان فرآیند را با سیری در نمودار P V توصیف کرد.
اهمیت بررسی انرژی داخلی
با اندازه گیریهای ترمودینامیکی ساده انتقال گرما و دمای متغیر سیستمهای گاز مولکولی ، میتوان آن قسمت از انرژی داخلی را که مربوط به چرخش و ارتعاش مولکول است بدست آورد؛ ولی این درجات آزادی در گازهای کامل صرفنظر میشود. با استفاده از این اندازه گیریها میتوان به برخی خصوصیات مولکولی ، از قبیل گشتاور لختی و طیف گسسته بسامدهای ارتعاشی مولکولی پی برد.
در مایعات و جامدات انرژی داخلی عمدتا همان انرژی پتانسیل برهمکنش بین اتمها است. تبادل گرما ، از طریق انقباض و انبساط که خود نتیجه تغییر حرکت اتمها است، مقدار این انرژی را تغییر میدهد، این حرکت در جامدات به صورت حرکت جمعی کوانتیده است. در جامدات رسانا انرژی الکترونها به صورت جنبشی و پتانسیل ، نیز به انرژی داخلی اضافه میشود. قیدهای کوانتومی ناشی از اصل طرد پاولی برای این انرژی در ترمودینامیک قابل تشخیص است.
تغییر انرژی داخلی
انرژی داخلی ممکن است با اعمال میدانهای الکتریکی و مغناطیسی روی سیستمهایی که دارای گشتاور دائمی یا القاییاند تغییر کند. در این موارد ، جز کار بینهایت کوچک برابر میشود E.dp یا µ.HdM که در آن E و H میدانهای اعمال شده و P و M به ترتیب دو قطبی الکتریکی و مغناطیسی سیستم هستند. اینها گشتاور متغیرهای ترمودینامیکی هستند که به مقادیر میدان و دما بستگی دارند.
یک مثال برای تغییر انرژی داخلی
مثال جالبی از تغییر انرژی داخلی توسط کار مغناطیسی ، سرد کردن از طریق وامغناطش بی دررو است. اگر میدان به مقدار متناهی کوچکی تقلیل یابد M و آنتروپی ثابتاند. اگر M ثابت باشد، کار مغناطیسی H.dM∫ برابر صفر میشود. چون فرآیند بی دررو است (φ = 0∆) ، پس u = 0∆. در این صورت با افزایش انرژی مغناطیسی منفی ، دمای سیستم باید کاهش یابد تا V ثابت بماند.
اندازه گیری انرژی داخلی
یکی از سیستمهایی که به عنوان مدل در خور توجه است، تابش الکترومغناطیسی در کاواکی به حجم V است. بنابر ترمودینامیک به هر یک از درجات آزادی این سیستم میتوان انرژی KT نسبت داد. تعداد درجات آزادی برابر تعداد مدهای درون کاواک است. درباره بسامد موج بین ν و ν + dν ، این تعداد برابر می شود با 8πVν²/C³)dV) که در آن C سرعت نور است. در گستره بسامدهای از نزدیکی صفر تا بسامدهای زیاد ، به تقریب خواهیم داشت:
U = (8πVKT/C³) ∫ν² dν
و معادله حالت به صورت PV = υ/3 در میآید. اگر چه هیچ یک از این دو نتیجه معنی فیزیکی ندارد، فقط با انجام آزمایش و مشاهده ثابتی که از حفره کوچکی از کاواک به صورت نمونهای از انرژی داخلی خارج میشود میتوان نشان داد که فاجعه فرابنفش که در این عبارت نهفته است اتفاق نمیافتد. این نمونه برداری نشان میدهد که
(U = 8πνh/C³ ∫ν³dν/(ehv/KT - 1
که در اینجا h ثابت پلانک است. این اولین موردی است که اندازه گیری انرژی داخلی در آن به تأیید اثرات کوانتومی منجر میشود. به بیان مناسبتر ، بنابر نظر آلبرت انیشتین ، این اندازه گیری وجود فوتونها و تابش کوانتیده را نشان داده و اساس انقلاب کوانتومی را پی ریزی کرد.
مجموع انرژیهای جنبشی و پتانسیل کلیه ذرههای یک جسم را انرژی درونی یا داخلی آن جسم مینامند.
نگاه اجمالی
اگر دستهای خود را به هم بمالید، مشاهده میکنید که دستهای شما گرم تر شده است. در این حالت انرژی جنبشی دستها کجا رفته است؟ چون دستها گرم تر شدهاند، میتوان نتیجه گرفت که انرژی درونی آنها افزایش یافته است. در نتیجه میتوان گفت که در اثر مالش انرژی جنبشی دستها به انرژی درونی آنها تبدیل شده است.
انرژی داخلی V و آنتروپی S ، دو تابع اساسی ، برای توصیف سیستمهای ترمودینامیکی در حالت تعادلاند، هر سیستم ماکروسکوپیکی که متشکل از انبوه اتم و مولکولهاست، از قانون بقای انرژی تبعیت میکند. حرکت بزرگ مقیاس سیستم از قانون بقای انرژی مکانیکی تبعیت میکند و در غیاب میدانهای الکترومغناطیسی ، انرژی باقی مانده در سیستمی که منزوی است پایسته میماند، این کمیت همان انرژی داخلی است.
سیر تحولی و رشد
از لحاظ تاریخی ، تشخیص اینکه کمیتی پایسته بصورت تابع تومودینامیکی انرژی (یعنی تابعی که از قانون پایستگی تبعیت میکند) وجود دارد، پیش از ظهور دیدگاه اتمی ماده حاصل شد. پس این مفهوم میبایستی منحصرا از طریق تجربیات ماکروسکوپیکی شکل گرفته باشد. آزمایشها و حدسیات اولیه بنجامین تامسون (کنت رامفورد) درباره ماهیت گرما او را به این نتیجه رساند که گرما نوعی حرکت است. کارهای تجربی بعدی جیمز پرسکارت ذول در تعیین معادل مکانیکی گرما و نظریه پرفلزی ویلیام تامسون (لرد کلوین) بطور قطع نشان دادند که انرژی سیستم ماکروسکوپیکی منزوی با به حساب آوردن گرما پایسته است. این همان قانون اول ترمودینامیک است و تابع پایسته نیز انرژی داخلی است.
مفهوم انرژی داخلی یا درونی
بنابر نظریه جنبشی مولکولی ، هر ماده از ذرات ریزی تشکیل شده است که با سرعتها و در نتیجه انرژیهای متفاوت در حرکت و جنبش هستند. علاوه بر این مانند مدل ارتعاش یک جسم جامد ، ذرههای جسم دارای انرژی پتانسیل نیز هستند. این انرژی به فنری که در مدل ارتعاشی اتمها را به هم متصل میکرد، مربوط است. مجموع انرژیهای جنبشی همه اتمها و مولکولهای تشکیل دهنده جسم یا دستگاه و انرژی پتانسیل مربوط به برهمکنشهای آنها ، بدون انرژیهای جنبشی و پتانسیل جسم یا دستگاه نسبت به بیرون خود یا انرژیهای هسته درون اتمهای آن.
ارتباط انرژی درونی با دما
انرژی درونی چای یک فنجان که مدتی مانده و سرد شده است، کمتر از وقتی است که چای داغ بوده است. چای یخ کرده دمای پایین تری دارد و چای داغ دمایش بالاتر است. به این ترتیب هر چه دمای جسمی بالاتر باشد، انرژی درونی آن بیشتر است. یعنی ذرههای آن دارای انرژی جنبشی و پتانسیل بیشتری هستند.
ارتباط انرژی جنبشی با دما
اگر انرژی جنبشی ذرات یک جسم را بر تعداد ذرات تشکیل دهنده جسم تقسیم کنیم، انرژی جنبشی متوسط یک ذره بدست میآید. انرژی جنبشی متوسط ذرات چای داغ که دمای بالاتری دارد، بیشتر از انرژی جنبشی متوسط ذرههای چای سرد شده است که دمای پایین تری دارد. لذا نتیجه میگیریم که دمای جسم با انرژی جنبشی متوسط ذرههای تشکیل دهنده آن متناسب است.
این امر در ابعاد اتمی یا ابعاد میکروسکوپی بسیار مهم و مورد توجه است. به عنوان مثال در مباحث ترمودینامیک و مکانیک آماری با استفاده از روابط خاصی این انرژی در موارد مختلف محاسبه شده و با توجه به به مقدار آن در مورد وضعیت سیستم بحث می گردد. بنابر این میتوان گفت که هر چه دمای جسم بالاتر رود ، انرژی جنبشی متوسط ذرههای آن نیز افزایش خواهد یافت.
انرژی جنبشی متوسط ذرههای دو جسم متفاوت که دمای یکسانی دارند، با هم برابر است. به عنوان یک مورد ملموس و قابل مشاهده میتوان به این مورد اشاره کرد که انرژی جنبشی متوسط ذرههای آبی که بوسیله یک لیوان از استخری برداشته شده است، با انرژی جنبشی متوسط ذرههای آب استخر برابر است. ولی به دلیل تفاوت تعداد ذرههای آب لیوان و آب استخر، انرژی جنبشی و در نتیجه انرژی درونی یکسانی ندارند. بلکه انرژی درونی آب لیوان به مراتب کمتر از انرژی درونی آب استخر است.
اختلاف انرژی داخلی
بطور مفهومی ، تفاوت انرژی داخلی بین دو حالت را میتوان به صورت کار مکانیکی انجام شدهای در نظر گرفت که سیستمی بی دررو (یعنی سیستمی با انزوای گرمایی) را از حالت (A) به حالت نهایی (B) میبرد. اگر نتوان فرآیندی بی دررو A → B یافت (یعنی اگر فرآیند برگشت ناپذیر باشد)، فرآیند B → A وجود دارد. بنابراین به روش مکانیکی میتوان تفاوت انرژی داخلی بین دو حالت را اندازه گیری کرده مشروط بر آنکه ماده از سیستم خارج یا به آن وارد نشود. طبیعتا فقط تفاوت انرژی داخلی است که کمیت در خور توجهی است و مقدار مطلق انرژی داخلی به خودی خود دارای معنی فیزیکی نیست.
بیان ریاضی انرژی داخلی
هر افزایش جزئی انرژی داخلی سیستم ، du برابر است با مجموع کار انجام شده روی سیستم đw و گرمای وارد شده đφ ، به سیستم (یعنی قانون اول ترمودینامیک) که به صورت du = đw + đφ نشان داده میشود. در این جا خط تیره کوچکی که روی نماد دیفرانسیل d که شکل đ وجود دارد، دیفرانسیل غیرحقیقی را نشان میدهد. ضرورت این انحرافات ریاضیاتی ، برای نشان دادن این واقعیت است که w و φ تابعهای حالت نیستند.
به عبارت دیگر ، کمیت گرما و کار جذب شده در سیستم بستگی به سیری دارد که سیستم میپیماید تا از حالت اولیه به حالت کنونیاش (یعنی حالت نهایی) برسد. در اکثر موارد حالت سیستمهای تک مؤلفهای مانند گاز را میتوان با دستگاه مختصاتی دکارتی نشان داد که در آن یکی از محورها فشار P و دیگری حجم V را نشان میدهد. در نتیجه میتوان فرآیند را با سیری در نمودار P V توصیف کرد.
اهمیت بررسی انرژی داخلی
با اندازه گیریهای ترمودینامیکی ساده انتقال گرما و دمای متغیر سیستمهای گاز مولکولی ، میتوان آن قسمت از انرژی داخلی را که مربوط به چرخش و ارتعاش مولکول است بدست آورد؛ ولی این درجات آزادی در گازهای کامل صرفنظر میشود. با استفاده از این اندازه گیریها میتوان به برخی خصوصیات مولکولی ، از قبیل گشتاور لختی و طیف گسسته بسامدهای ارتعاشی مولکولی پی برد.
در مایعات و جامدات انرژی داخلی عمدتا همان انرژی پتانسیل برهمکنش بین اتمها است. تبادل گرما ، از طریق انقباض و انبساط که خود نتیجه تغییر حرکت اتمها است، مقدار این انرژی را تغییر میدهد، این حرکت در جامدات به صورت حرکت جمعی کوانتیده است. در جامدات رسانا انرژی الکترونها به صورت جنبشی و پتانسیل ، نیز به انرژی داخلی اضافه میشود. قیدهای کوانتومی ناشی از اصل طرد پاولی برای این انرژی در ترمودینامیک قابل تشخیص است.
تغییر انرژی داخلی
انرژی داخلی ممکن است با اعمال میدانهای الکتریکی و مغناطیسی روی سیستمهایی که دارای گشتاور دائمی یا القاییاند تغییر کند. در این موارد ، جز کار بینهایت کوچک برابر میشود E.dp یا µ.HdM که در آن E و H میدانهای اعمال شده و P و M به ترتیب دو قطبی الکتریکی و مغناطیسی سیستم هستند. اینها گشتاور متغیرهای ترمودینامیکی هستند که به مقادیر میدان و دما بستگی دارند.
یک مثال برای تغییر انرژی داخلی
مثال جالبی از تغییر انرژی داخلی توسط کار مغناطیسی ، سرد کردن از طریق وامغناطش بی دررو است. اگر میدان به مقدار متناهی کوچکی تقلیل یابد M و آنتروپی ثابتاند. اگر M ثابت باشد، کار مغناطیسی H.dM∫ برابر صفر میشود. چون فرآیند بی دررو است (φ = 0∆) ، پس u = 0∆. در این صورت با افزایش انرژی مغناطیسی منفی ، دمای سیستم باید کاهش یابد تا V ثابت بماند.
اندازه گیری انرژی داخلی
یکی از سیستمهایی که به عنوان مدل در خور توجه است، تابش الکترومغناطیسی در کاواکی به حجم V است. بنابر ترمودینامیک به هر یک از درجات آزادی این سیستم میتوان انرژی KT نسبت داد. تعداد درجات آزادی برابر تعداد مدهای درون کاواک است. درباره بسامد موج بین ν و ν + dν ، این تعداد برابر می شود با 8πVν²/C³)dV) که در آن C سرعت نور است. در گستره بسامدهای از نزدیکی صفر تا بسامدهای زیاد ، به تقریب خواهیم داشت:
U = (8πVKT/C³) ∫ν² dν
و معادله حالت به صورت PV = υ/3 در میآید. اگر چه هیچ یک از این دو نتیجه معنی فیزیکی ندارد، فقط با انجام آزمایش و مشاهده ثابتی که از حفره کوچکی از کاواک به صورت نمونهای از انرژی داخلی خارج میشود میتوان نشان داد که فاجعه فرابنفش که در این عبارت نهفته است اتفاق نمیافتد. این نمونه برداری نشان میدهد که
(U = 8πνh/C³ ∫ν³dν/(ehv/KT - 1
که در اینجا h ثابت پلانک است. این اولین موردی است که اندازه گیری انرژی داخلی در آن به تأیید اثرات کوانتومی منجر میشود. به بیان مناسبتر ، بنابر نظر آلبرت انیشتین ، این اندازه گیری وجود فوتونها و تابش کوانتیده را نشان داده و اساس انقلاب کوانتومی را پی ریزی کرد.
مرکز انجمنهای تخصصی گنجینه دانش
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]

-
- پست: 5234
- تاریخ عضویت: پنجشنبه ۲۵ خرداد ۱۳۸۵, ۲:۴۷ ب.ظ
- سپاسهای ارسالی: 1747 بار
- سپاسهای دریافتی: 4179 بار
- تماس:
دما
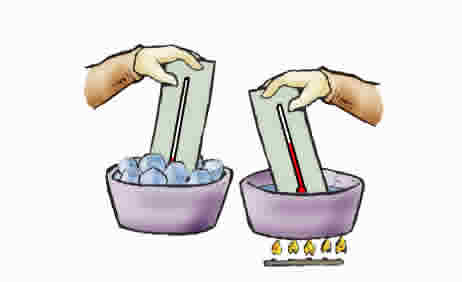
دمای یک سیستم ویژگی است که تعیین میکند آیا یک سیستم با سیستمهای دیگر در تعادل گرمایی قرار دارد یا خیر.
دید کلی
مفاهیم داغ و سرد برای انسان ، مانند هر موجود زنده دیگر ذاتی است و دمای محیط مجاور را بیلیونها عصبی که به سطح پوسته میرسند، به مغز خبر میدهند. اما پاسخ فیزیولوژیکی به دما اغلب گمراه کننده است و کسی که چشمش بسته است نمیتواند بگوید که آیا دستش با اتوی بسیار داغ ، سوخته یا به وسیله یک تکه یخ خشک شده است. در هر دو حالت احساسی پدید میآید، زیرا هر دو عینا پاسخ فیزیولوژیکی به آسیبی هستند که به نسج رسیده است.
یک آزمایش ساده
دو ظرف یکسان انتخاب کرده ، در یکی آب گرم و در دیگری آب سرد بریزید. حال یک دست خود را در آب گرم و دست دیگر را در آب سرد فرو برید. حال هر دو دست را در آب نیمگرم وارد کنید. احساس شما چیست؟
قطعا دستی که ابتدا در آب گرم بوده است، آب نیمگرم را سردتر و دست دیگر آن را گرمتر احساس خواهد کرد. بنابراین با این آزمایش ساده میتوان نتیجه گرفت که قضاوت ما در مورد دما میتواند نسبتا گمراه کننده باشد. علاوه بر این گستره حس دمایی ما محدود است و ما به یک معیار معین و عددی برای تعیین دما نیاز داریم.
دماسنجهای اولیه
نخستین وسیله واقعی علمی برای اندازه گیری دما در سال 1592 توسط گالیله اختراع شد. وی برای این منظور یک بطری شیشهای گردنباریک انتخاب کرده بود. بطری با آب رنگین تا نیمه پر شده و وارونه در یک ظرف محتوی آب رنگین قرار گرفته بود. با تغییر دما ، هوای محتوی شکم بطری منبسط یا منقبض میشد و ستون آب در گردن بطری بالا یا پایین میرفت. در این وسیله ، گالیله توجه نداشت که مقیاس برای سنجش دما بکار ببرد، بطوری که وسیله وی ، بیشتر جنبه دما نما داشت تا جنبه دماسنج.
در سال 1635 ، فردیناند توسکانی ، که به علوم علاقهمند بود، دماسنجی ساخت که درآن از الکل استفاده کرد و سر لوله را چنان محکم بست که الکل نتواند تبخیر شود. سرانجام ، در سال 1640 ، دانشمندان آکادمی لینچی ، در ایتالیا ، نمونهای از دماسنجهای جدیدی را ساختند که در آن جیوه به کار برده و هوا را دست کم تا حدودی ، از قسمت بالای لوله بسته خارج کرده بودند.
توجه به این نکته جالب است که در حدود نیم قرن طول کشید تا دماسنج کاملا تکامل یافت و حال آنکه میان کشف امواج الکترومغناطیسی و ساختن نخستین تلگراف بیسیم ، یا میان کشف اورانیوم و نخستین بمب اتمی چند سالی بیشتر طول نکشید.
اندازه گیری دما
برای تعیین یک مقیاس تجربی دما ، سیستمی با مختصات xy را به عنوان استاندارد که ما آن را دماسنج مینامیم، انتخاب میکنیم و مجموعه قواعدی را برای نسبت دادن یک مقدار عددی به دمای وابسته به هر کدام از منحنیهای همدمای آن ، اختیار میکنیم. به هر سیستم دیگری که با دماسنج در تعادل گرمایی باشد، همین عدد را برای دما نسبت میدهیم.
قوانین گازها
همان وقت که اسحاق نیوتن در کمبریج درباره نور و جاذبه میاندیشید، یک نفر انگلیسی دیگر به نام رابرت بویل ، در آکسفورد سرگرم مطالعه در باب خواص مکانیکی و تراکمپذیری هوا و سایر گازها بود. بویل که خبر اختراع گلوله سربی اوتوفون گریکه را شنیده بود، طرح خویش را تکمیل کرد و دست به کار آزمایشهایی برای اندازه گیری حجم هوا در فشار کم و زیاد شد.
نتیجه کارهای وی چیزی است که اکنون به قانون بویل-ماریوت معروف است و بیان میکند که حجم مقدار معینی از هر گاز در دمای معین با فشاری که بر آن گاز وارد میشود، بطور معکوس متناسب است با فشاری که بر آن گاز وارد میشود.
حدود یک قرن بعد ، ژوزف گیلوساک فرانسوی ، در ضمن مطالعه انبساط گازها ، قانون مهم دیگری پیدا کرد که بیان آن این است: فشار هر گاز محتوی در حجم معین به ازای هر یک درجه سانتیگراد افزایش دما ، به اندازه 273/1 حجم اولیهاش افزایش مییابد. همین قانون را یک فرانسوی دیگر به نام ژاک شارل ، دو سال پیش از آن کشف کرده بود و از این رو اغلب آن را قانون شارل-گیلوساک مینامند. این دو قانون مبنای ساخت دماسنجهای گازی قرار گرفت.

دمای یک سیستم ویژگی است که تعیین میکند آیا یک سیستم با سیستمهای دیگر در تعادل گرمایی قرار دارد یا خیر.

دید کلی
مفاهیم داغ و سرد برای انسان ، مانند هر موجود زنده دیگر ذاتی است و دمای محیط مجاور را بیلیونها عصبی که به سطح پوسته میرسند، به مغز خبر میدهند. اما پاسخ فیزیولوژیکی به دما اغلب گمراه کننده است و کسی که چشمش بسته است نمیتواند بگوید که آیا دستش با اتوی بسیار داغ ، سوخته یا به وسیله یک تکه یخ خشک شده است. در هر دو حالت احساسی پدید میآید، زیرا هر دو عینا پاسخ فیزیولوژیکی به آسیبی هستند که به نسج رسیده است.
یک آزمایش ساده
دو ظرف یکسان انتخاب کرده ، در یکی آب گرم و در دیگری آب سرد بریزید. حال یک دست خود را در آب گرم و دست دیگر را در آب سرد فرو برید. حال هر دو دست را در آب نیمگرم وارد کنید. احساس شما چیست؟
قطعا دستی که ابتدا در آب گرم بوده است، آب نیمگرم را سردتر و دست دیگر آن را گرمتر احساس خواهد کرد. بنابراین با این آزمایش ساده میتوان نتیجه گرفت که قضاوت ما در مورد دما میتواند نسبتا گمراه کننده باشد. علاوه بر این گستره حس دمایی ما محدود است و ما به یک معیار معین و عددی برای تعیین دما نیاز داریم.
دماسنجهای اولیه
نخستین وسیله واقعی علمی برای اندازه گیری دما در سال 1592 توسط گالیله اختراع شد. وی برای این منظور یک بطری شیشهای گردنباریک انتخاب کرده بود. بطری با آب رنگین تا نیمه پر شده و وارونه در یک ظرف محتوی آب رنگین قرار گرفته بود. با تغییر دما ، هوای محتوی شکم بطری منبسط یا منقبض میشد و ستون آب در گردن بطری بالا یا پایین میرفت. در این وسیله ، گالیله توجه نداشت که مقیاس برای سنجش دما بکار ببرد، بطوری که وسیله وی ، بیشتر جنبه دما نما داشت تا جنبه دماسنج.
در سال 1635 ، فردیناند توسکانی ، که به علوم علاقهمند بود، دماسنجی ساخت که درآن از الکل استفاده کرد و سر لوله را چنان محکم بست که الکل نتواند تبخیر شود. سرانجام ، در سال 1640 ، دانشمندان آکادمی لینچی ، در ایتالیا ، نمونهای از دماسنجهای جدیدی را ساختند که در آن جیوه به کار برده و هوا را دست کم تا حدودی ، از قسمت بالای لوله بسته خارج کرده بودند.
توجه به این نکته جالب است که در حدود نیم قرن طول کشید تا دماسنج کاملا تکامل یافت و حال آنکه میان کشف امواج الکترومغناطیسی و ساختن نخستین تلگراف بیسیم ، یا میان کشف اورانیوم و نخستین بمب اتمی چند سالی بیشتر طول نکشید.
اندازه گیری دما
برای تعیین یک مقیاس تجربی دما ، سیستمی با مختصات xy را به عنوان استاندارد که ما آن را دماسنج مینامیم، انتخاب میکنیم و مجموعه قواعدی را برای نسبت دادن یک مقدار عددی به دمای وابسته به هر کدام از منحنیهای همدمای آن ، اختیار میکنیم. به هر سیستم دیگری که با دماسنج در تعادل گرمایی باشد، همین عدد را برای دما نسبت میدهیم.
قوانین گازها
همان وقت که اسحاق نیوتن در کمبریج درباره نور و جاذبه میاندیشید، یک نفر انگلیسی دیگر به نام رابرت بویل ، در آکسفورد سرگرم مطالعه در باب خواص مکانیکی و تراکمپذیری هوا و سایر گازها بود. بویل که خبر اختراع گلوله سربی اوتوفون گریکه را شنیده بود، طرح خویش را تکمیل کرد و دست به کار آزمایشهایی برای اندازه گیری حجم هوا در فشار کم و زیاد شد.
نتیجه کارهای وی چیزی است که اکنون به قانون بویل-ماریوت معروف است و بیان میکند که حجم مقدار معینی از هر گاز در دمای معین با فشاری که بر آن گاز وارد میشود، بطور معکوس متناسب است با فشاری که بر آن گاز وارد میشود.
حدود یک قرن بعد ، ژوزف گیلوساک فرانسوی ، در ضمن مطالعه انبساط گازها ، قانون مهم دیگری پیدا کرد که بیان آن این است: فشار هر گاز محتوی در حجم معین به ازای هر یک درجه سانتیگراد افزایش دما ، به اندازه 273/1 حجم اولیهاش افزایش مییابد. همین قانون را یک فرانسوی دیگر به نام ژاک شارل ، دو سال پیش از آن کشف کرده بود و از این رو اغلب آن را قانون شارل-گیلوساک مینامند. این دو قانون مبنای ساخت دماسنجهای گازی قرار گرفت.

مرکز انجمنهای تخصصی گنجینه دانش
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]

-
- پست: 5234
- تاریخ عضویت: پنجشنبه ۲۵ خرداد ۱۳۸۵, ۲:۴۷ ب.ظ
- سپاسهای ارسالی: 1747 بار
- سپاسهای دریافتی: 4179 بار
- تماس:
انواع دماسنجها
دماسنج گازی
جنس ، ساختمان و ابعاد دماسنج در ادارات و موسسات مختلف سراسر دنیا که این دستگاه را بکار میبرند، تفاوت دارد و به طبیعت گاز و گستره دمایی که دماسنج برای آن در نظر گرفته شده است، بستگی دارد. این دماسنج شامل حبابی از جنس شیشه ، چینی ، کوارتز ، پلاتین یا پلاتین ـ ایریدیم ، ( بسته به گستره دمایی که دماسنج در آن بکار میرود )، میباشد که به وسیله یک لوله موئین به فشارسنج جیوهای متصل است. این دماسنج براساس دو قانون ذکر شده در مورد گاز کامل کار میکند.
دماسنج با مقاومت الکتریکی
دماسنج مقاومتی به صورت یک سیم بلند و ظریف است، معمولا آن را به دور یک قاب نازک میپیچند تا از فشار ناشی از تغییر طول سیم که در اثر انقباض آن در موقع سرد شدن پیش میآید، جلوگیری کند. در شرایط ویژه میتوان سیم را به دور جسمی که منظور اندازه گیری دمای آن است پیچید یا در داخل آن قرار داد.
در گستره دمای خیلی پایین ، دماسنجهای مقاومتی معمولا از مقاومتهای کوچک رادیویی با ترکیب کربن یا بلور ژرمانیوم که ناخالصی آن آرسنیک است و جسم حاصل در درون یک کپسول مسدود شده پر از هلیوم قرار دارد، تشکیل میشوند. این دماسنج را میتوان بر روی سطح جسمی که بمنظور اندازه گیری دمای آن است سوار کرد یا در حفرهای که برای این منظور ایجاد شده است، قرار داد.
دماسنج مقاومتی پلاتین را میتوان برای کارهای خیلی دقیق در گستره 253– تا 1200 درجه سانتیگراد بکار برد.
ترموکوپل
ترموکوپل وسیله دیگری است که برای اندازه گیری دما مورد استفاده قرار میگیرد. در این نوع دماسنج از خاصیت انبساط و انقباض اجسام جامد استفاده میگردد. گستره یک ترموکوپل بستگی به موادی دارد که ترموکوپل از آن ساخته شده است. گستره یک ترموکوپل پلاتنیوم ـ رودیوم که 10 درصد پلاتینیوم دارد، از صفر تا 1600 درجه سانتیگراد است.
مزیت ترموکوپل در این است که بخاطر جرم کوچک ، خیلی سریع با سیستمی که اندازه گیری دمای آن مورد نظر است، به حال تعادل گرمایی در میآید. لذا تغییرات دما به آسانی بر آن اثر میکند، ولی دقت دماسنج مقاومتی پلاتین را ندارد.
واحد اندازه گیری دما
* کلوین: کلوین مقیاس بنیادی دما در علوم است که سایر مقیاسها بر حسب آن تعریف میشوند.
* سلیسیوس یا سانتیگراد: مقیاس سلیسیوس بر اساس نقطه سه گانه آب میباشد. اگر t نشاندهنده دمای سلیسیوس و T نشاندهنده دمای کلوین باشد، در اینصورت داریم: 273.15 - t =T
* فارنهایت: این مقیاس هنوز هم در بعضی از کشورهای انگلیسیزبان به کار میرود و در کارهای علمی استفاده نمیشود.
دماسنج گازی
جنس ، ساختمان و ابعاد دماسنج در ادارات و موسسات مختلف سراسر دنیا که این دستگاه را بکار میبرند، تفاوت دارد و به طبیعت گاز و گستره دمایی که دماسنج برای آن در نظر گرفته شده است، بستگی دارد. این دماسنج شامل حبابی از جنس شیشه ، چینی ، کوارتز ، پلاتین یا پلاتین ـ ایریدیم ، ( بسته به گستره دمایی که دماسنج در آن بکار میرود )، میباشد که به وسیله یک لوله موئین به فشارسنج جیوهای متصل است. این دماسنج براساس دو قانون ذکر شده در مورد گاز کامل کار میکند.
دماسنج با مقاومت الکتریکی
دماسنج مقاومتی به صورت یک سیم بلند و ظریف است، معمولا آن را به دور یک قاب نازک میپیچند تا از فشار ناشی از تغییر طول سیم که در اثر انقباض آن در موقع سرد شدن پیش میآید، جلوگیری کند. در شرایط ویژه میتوان سیم را به دور جسمی که منظور اندازه گیری دمای آن است پیچید یا در داخل آن قرار داد.
در گستره دمای خیلی پایین ، دماسنجهای مقاومتی معمولا از مقاومتهای کوچک رادیویی با ترکیب کربن یا بلور ژرمانیوم که ناخالصی آن آرسنیک است و جسم حاصل در درون یک کپسول مسدود شده پر از هلیوم قرار دارد، تشکیل میشوند. این دماسنج را میتوان بر روی سطح جسمی که بمنظور اندازه گیری دمای آن است سوار کرد یا در حفرهای که برای این منظور ایجاد شده است، قرار داد.
دماسنج مقاومتی پلاتین را میتوان برای کارهای خیلی دقیق در گستره 253– تا 1200 درجه سانتیگراد بکار برد.
ترموکوپل
ترموکوپل وسیله دیگری است که برای اندازه گیری دما مورد استفاده قرار میگیرد. در این نوع دماسنج از خاصیت انبساط و انقباض اجسام جامد استفاده میگردد. گستره یک ترموکوپل بستگی به موادی دارد که ترموکوپل از آن ساخته شده است. گستره یک ترموکوپل پلاتنیوم ـ رودیوم که 10 درصد پلاتینیوم دارد، از صفر تا 1600 درجه سانتیگراد است.
مزیت ترموکوپل در این است که بخاطر جرم کوچک ، خیلی سریع با سیستمی که اندازه گیری دمای آن مورد نظر است، به حال تعادل گرمایی در میآید. لذا تغییرات دما به آسانی بر آن اثر میکند، ولی دقت دماسنج مقاومتی پلاتین را ندارد.
واحد اندازه گیری دما
* کلوین: کلوین مقیاس بنیادی دما در علوم است که سایر مقیاسها بر حسب آن تعریف میشوند.
* سلیسیوس یا سانتیگراد: مقیاس سلیسیوس بر اساس نقطه سه گانه آب میباشد. اگر t نشاندهنده دمای سلیسیوس و T نشاندهنده دمای کلوین باشد، در اینصورت داریم: 273.15 - t =T
* فارنهایت: این مقیاس هنوز هم در بعضی از کشورهای انگلیسیزبان به کار میرود و در کارهای علمی استفاده نمیشود.
مرکز انجمنهای تخصصی گنجینه دانش
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]

-
- پست: 5234
- تاریخ عضویت: پنجشنبه ۲۵ خرداد ۱۳۸۵, ۲:۴۷ ب.ظ
- سپاسهای ارسالی: 1747 بار
- سپاسهای دریافتی: 4179 بار
- تماس:
صفر مطلق
دید کلی
نقطه مرجع در مقیاس دمای مطلق 273,15- سانتیگراد است. این نقطه را صفر مطلق میگویند، معنای آن تنها پس ار روشن شدن ارتباط منشا گاز با انرژی جنبشی اتمهای آن با توجه به نظریه جنبشی گازها ، روشن شد. این نظریه بیان میکند که حرکت اتمها در صفر مطلق به کلی متوقف میشود، ولی این توضیح درست نیست. در واقع مکانیک کلاسیک قادر به توضیح این پدیده نیست، ولی مکانیک کوانتومی آن را به خوبی توضیح میدهد.
فیزیک در صفر مطلق
نظریه جنبشی گازها بیان میکند که در صفر مطلق حرکت اتمها به کلی متوقف میشود و دمای مطلق T تنها معیاری از اندازه انرژی جنبشی اتمهاست و بس. اما این توضیح هر چند ساده واضح است، درست نیست. اکثر دماها در فلزات حتی در دمای T = 0 نیز با سرعتهای بالا حرکت میکنند.
مکانیک کوانتومی برای خیلی از مفاهیم توضیحات طبیعی دارد از جمله دمای مطلق و صفر مطلق.
دید کلی
نقطه مرجع در مقیاس دمای مطلق 273,15- سانتیگراد است. این نقطه را صفر مطلق میگویند، معنای آن تنها پس ار روشن شدن ارتباط منشا گاز با انرژی جنبشی اتمهای آن با توجه به نظریه جنبشی گازها ، روشن شد. این نظریه بیان میکند که حرکت اتمها در صفر مطلق به کلی متوقف میشود، ولی این توضیح درست نیست. در واقع مکانیک کلاسیک قادر به توضیح این پدیده نیست، ولی مکانیک کوانتومی آن را به خوبی توضیح میدهد.
فیزیک در صفر مطلق
نظریه جنبشی گازها بیان میکند که در صفر مطلق حرکت اتمها به کلی متوقف میشود و دمای مطلق T تنها معیاری از اندازه انرژی جنبشی اتمهاست و بس. اما این توضیح هر چند ساده واضح است، درست نیست. اکثر دماها در فلزات حتی در دمای T = 0 نیز با سرعتهای بالا حرکت میکنند.
مکانیک کوانتومی برای خیلی از مفاهیم توضیحات طبیعی دارد از جمله دمای مطلق و صفر مطلق.
مرکز انجمنهای تخصصی گنجینه دانش
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]

-
- پست: 5234
- تاریخ عضویت: پنجشنبه ۲۵ خرداد ۱۳۸۵, ۲:۴۷ ب.ظ
- سپاسهای ارسالی: 1747 بار
- سپاسهای دریافتی: 4179 بار
- تماس:
مکانیک کوانتمی
برای ادامه بحث باید قدری اطلاعات کوانتومی داشته باشیم که متأسفانه آن را با چند کلمه نمیتوان بیان کرد، ولی سعی کنیم واقعیات را بدون اثبات بیان و تعداد اطلاعات را به حداقل برسانیم. اگر بخواهیم از رفتار الکترون در میدان مغناطیسی اطلاع داشته باشیم مکانیک کوانتومی توصیف زیر را ارائه میدهد:
الکترون را میتوان با فرفره چرخان مقایسه کرد (هر چند این مقایسه خیلی درست نیست). بهتر است بگوییم که الکترون ، همانند فرفره چرخان ، دارای تکلانه زاویهای ذاتی به نام اسپین است، بدون اینکه در جزئیات چرخش بحث کنیم اسپین الکترون به گشتاور مغناطیسی ذاتی آن مربوط است. الکترون در میدان مغناطیسی مانند آهنربا رفتار میکند.
اگر الکترون در میدان مغناطیسی ثابت قرار گیرد بنا به قوانین مکانیک کوانتومی اسپین آن میتواند یا در امتداد راستای میدان قرار گیرد و یا در جهت مخالف آن. راستای گشتاور دو مغناطیسی الکترون در جهت مخالف اسپین است: از اینرو همانند اسپین میتواند دو تصویر در جهت میدان مغناطیسی داشته باشد. اگر میدان هم راستا باشند، این تصویرز برابر است با µ0- و اگر در راستای هم باشند، برابر است با µ0+ که µ0>0 ، کمیت µ مگنتون بور نام دارد. اگر شدت میدان مغناطیسی H باشد، انرژی پتانسیل یک الکترون در این میدان برابر میشود با µ0H یا µ0H- ، سرانجام میتوان گفت الکترون در میدان مغناطیسی میتواند دو حالت داشته باشد، انرژی این حالتها برابر است با µ0H یا µ0H-.
اکنون دستگاهی متشکل از تعداد زیادی الکترون را که در نقاط مختلف فضا ثابت شدهاند در نظر میگیریم. به عنوان مثال میتوان تعداد زیادی اتم را که هر کدام چند الکترون دارند، در نظر گرفت. انرژی این دستگاه در میدان مغناطیسی را تعداد الکترون نهایی که اسپین آنها در راستای میدان و مخالف آن هستند، تعیین میکنند.
برای ادامه بحث باید قدری اطلاعات کوانتومی داشته باشیم که متأسفانه آن را با چند کلمه نمیتوان بیان کرد، ولی سعی کنیم واقعیات را بدون اثبات بیان و تعداد اطلاعات را به حداقل برسانیم. اگر بخواهیم از رفتار الکترون در میدان مغناطیسی اطلاع داشته باشیم مکانیک کوانتومی توصیف زیر را ارائه میدهد:
الکترون را میتوان با فرفره چرخان مقایسه کرد (هر چند این مقایسه خیلی درست نیست). بهتر است بگوییم که الکترون ، همانند فرفره چرخان ، دارای تکلانه زاویهای ذاتی به نام اسپین است، بدون اینکه در جزئیات چرخش بحث کنیم اسپین الکترون به گشتاور مغناطیسی ذاتی آن مربوط است. الکترون در میدان مغناطیسی مانند آهنربا رفتار میکند.
اگر الکترون در میدان مغناطیسی ثابت قرار گیرد بنا به قوانین مکانیک کوانتومی اسپین آن میتواند یا در امتداد راستای میدان قرار گیرد و یا در جهت مخالف آن. راستای گشتاور دو مغناطیسی الکترون در جهت مخالف اسپین است: از اینرو همانند اسپین میتواند دو تصویر در جهت میدان مغناطیسی داشته باشد. اگر میدان هم راستا باشند، این تصویرز برابر است با µ0- و اگر در راستای هم باشند، برابر است با µ0+ که µ0>0 ، کمیت µ مگنتون بور نام دارد. اگر شدت میدان مغناطیسی H باشد، انرژی پتانسیل یک الکترون در این میدان برابر میشود با µ0H یا µ0H- ، سرانجام میتوان گفت الکترون در میدان مغناطیسی میتواند دو حالت داشته باشد، انرژی این حالتها برابر است با µ0H یا µ0H-.
اکنون دستگاهی متشکل از تعداد زیادی الکترون را که در نقاط مختلف فضا ثابت شدهاند در نظر میگیریم. به عنوان مثال میتوان تعداد زیادی اتم را که هر کدام چند الکترون دارند، در نظر گرفت. انرژی این دستگاه در میدان مغناطیسی را تعداد الکترون نهایی که اسپین آنها در راستای میدان و مخالف آن هستند، تعیین میکنند.
مرکز انجمنهای تخصصی گنجینه دانش
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]

-
- پست: 5234
- تاریخ عضویت: پنجشنبه ۲۵ خرداد ۱۳۸۵, ۲:۴۷ ب.ظ
- سپاسهای ارسالی: 1747 بار
- سپاسهای دریافتی: 4179 بار
- تماس:
مقایسه دستگاه الکترونها در میدان مغناطیسی و گاز کامل
دستگاهی از الکترونها با گشتاور مغناطیسی را میتوان با گاز کامل مقایسه کرد و انرژی الکترون در میدان مغناطیسی نقش سرعت (انرژی جنبشی) اتمها را بازی میکند. اما به انرژی جنبشی میتوان هر مقدار مثبتی را نسبت داد، در حالی که انرژی در میدان مغناطیسی ، فقط دو مقدار به خود میگیرد. جالب است بدانید که این قید قانون پایه آمار را تغییر نمیدهد و در ترازمندی گرمایی ، احتمال یافتن ذرهای در حالت انرژی ε با تابع نمایی (exp(-ε/kt متناسب است.
در اینجا نیز همچون گاز ، لازم است ترازمندی گرمایی اتمها واقعا دست یافتنی باشد، بنابراین (مانند برخورد اتمها در گاز کامل) گشتاورهای مغناطیسی باید با یکدیگر برهمکنش داشته باشند. اگر این شرط تأمین شود، قانون آمار بدون توجه به ساز و کار خاصی که دستگاه را به ترازمندی گرمایی میکشاند، حکم فرما خواهد بود.
انرژی الکترون در میدان مغناطیسی:
µ0H: اسپین در امتداد میدان
µ0H-: اسپین در جهت مخالف میدان
پس با توجه به آنچه گفته شد در ترازمندی گرمایی احتمال یافتن ذره در حالت اسپین در امتداد میدان (exp(µ0H/kT است، یعنی در ترازمندی گرمایی تعداد الکترونها با اسپین مخالف جهت میدان از تعداد الکترونها با اسپین در جهت میدان بیشتر است. همانطور که مشاهده میکنید، حالت ترازمندی پایایی دستگاه تنها با تک پارامتر T ، یعنی دمای مطلق آن تعیین میشود.
عقربههای مغناطیسی
اکنون فرض کنید که به جای الکترونهای دارای گشتاور در مغناطیسی ، تعدادی عقربه مغناطیسی داریم که بطور کاتورهای پراکندهاند. چون عقربههای مغناطیسی باید سمت شمال قرار گیرند، آنها با دامنه یکسان در راستای شمال - جنوب به نوسان در میآیند. اگر محور عقربهها اصطکاکی نداشت و نیز میان عقربهها جاذبهای موجود نبود، این نوسانها بطور نامحدود ادامه پیدا میکردند. در واقع ، سرانجام عقربهها از نوسان باز میایستند، زیرا بر اثر اصطکاک محور ، انرژی مصرف میشود و همه عقربهها به سمت شمال قرار میگیرند.
به علاوه ، عقربههای آهنربا روی یکدیگر نیز تأثیر میگذارند. حرکتشان به یکدیگر جفت شده است، یعنی میتوانند انرژی به عقربههای دیگر انتقال دهند. بدین طریق میتوان در رفتار عقربهها مدلی از چگونگی رسیدن دستگاه اسپینها به ترازمندی بازیافت. محورها نقش مرداب گرما را بازی میکنند که انرژی جنبشی عقربهها به آنها منتقل میشود. عقربههای ساکن به دستگاه اسپینها ، در دمای T=0 شباهت دارد. دما به صفر میرسدف زیرا انرژی همواره از عقربهها به محورها انتقال مییابد، بعد از اینکه همه انرژی انتقال یافت ترازمندی برقرار میشود.
با مطالعه در مییابیم که عقربههای مغناطیسی کاملا نمیایستند، بلکه به سبب بمباران دائم توسط مولکولهای هوا و لرزش خفیف محورهایشان ، با دامنههای خیلی کوچک نوسان میکنند. از اینرو انرژی نمیتواند تا صفر تنزل کند و در میانگین برابر kT باقی میماند. این حرکت را حرکت براونی گویند.
مدل عقربههای آهنربا و مفهوم صفر مطلق
در راستای ممکن اسپین در هر دما، احتمالهای متفاوت رخ میدهند. در دماهای خیلی پایین تقریبا همه الکترونها در تراز پایینتر جمع میشوند. یعنی اسپینهای آنها در راستای مخالف میدان قرار میگیرند. تراز بالاتر ، تقریبا تهی ، یعنی خالی از جمعیت میماند. هر چه دما بالاتر باشد، تراز بالاتر "پرجمعیت" میشود. به عنوان مثال در دماهای خیلی بالا (ε << KT) هر دو تصویر اسپین احتمال تقریبا برابر دارند. اگر دما پایین بیاید، بخش بزرگ و رو به افزایشی از اسپین الکترونها در راستای مخالف قرار میگیرند. اگر T = 0 باشد، اسپین همه الکترونها در راستای مخالف میدان قرار میگیرند. این حالت دستگاه با دمای صفر مطلق متناظر است.
دستگاهی از الکترونها با گشتاور مغناطیسی را میتوان با گاز کامل مقایسه کرد و انرژی الکترون در میدان مغناطیسی نقش سرعت (انرژی جنبشی) اتمها را بازی میکند. اما به انرژی جنبشی میتوان هر مقدار مثبتی را نسبت داد، در حالی که انرژی در میدان مغناطیسی ، فقط دو مقدار به خود میگیرد. جالب است بدانید که این قید قانون پایه آمار را تغییر نمیدهد و در ترازمندی گرمایی ، احتمال یافتن ذرهای در حالت انرژی ε با تابع نمایی (exp(-ε/kt متناسب است.
در اینجا نیز همچون گاز ، لازم است ترازمندی گرمایی اتمها واقعا دست یافتنی باشد، بنابراین (مانند برخورد اتمها در گاز کامل) گشتاورهای مغناطیسی باید با یکدیگر برهمکنش داشته باشند. اگر این شرط تأمین شود، قانون آمار بدون توجه به ساز و کار خاصی که دستگاه را به ترازمندی گرمایی میکشاند، حکم فرما خواهد بود.
انرژی الکترون در میدان مغناطیسی:
µ0H: اسپین در امتداد میدان
µ0H-: اسپین در جهت مخالف میدان
پس با توجه به آنچه گفته شد در ترازمندی گرمایی احتمال یافتن ذره در حالت اسپین در امتداد میدان (exp(µ0H/kT است، یعنی در ترازمندی گرمایی تعداد الکترونها با اسپین مخالف جهت میدان از تعداد الکترونها با اسپین در جهت میدان بیشتر است. همانطور که مشاهده میکنید، حالت ترازمندی پایایی دستگاه تنها با تک پارامتر T ، یعنی دمای مطلق آن تعیین میشود.
عقربههای مغناطیسی
اکنون فرض کنید که به جای الکترونهای دارای گشتاور در مغناطیسی ، تعدادی عقربه مغناطیسی داریم که بطور کاتورهای پراکندهاند. چون عقربههای مغناطیسی باید سمت شمال قرار گیرند، آنها با دامنه یکسان در راستای شمال - جنوب به نوسان در میآیند. اگر محور عقربهها اصطکاکی نداشت و نیز میان عقربهها جاذبهای موجود نبود، این نوسانها بطور نامحدود ادامه پیدا میکردند. در واقع ، سرانجام عقربهها از نوسان باز میایستند، زیرا بر اثر اصطکاک محور ، انرژی مصرف میشود و همه عقربهها به سمت شمال قرار میگیرند.
به علاوه ، عقربههای آهنربا روی یکدیگر نیز تأثیر میگذارند. حرکتشان به یکدیگر جفت شده است، یعنی میتوانند انرژی به عقربههای دیگر انتقال دهند. بدین طریق میتوان در رفتار عقربهها مدلی از چگونگی رسیدن دستگاه اسپینها به ترازمندی بازیافت. محورها نقش مرداب گرما را بازی میکنند که انرژی جنبشی عقربهها به آنها منتقل میشود. عقربههای ساکن به دستگاه اسپینها ، در دمای T=0 شباهت دارد. دما به صفر میرسدف زیرا انرژی همواره از عقربهها به محورها انتقال مییابد، بعد از اینکه همه انرژی انتقال یافت ترازمندی برقرار میشود.
با مطالعه در مییابیم که عقربههای مغناطیسی کاملا نمیایستند، بلکه به سبب بمباران دائم توسط مولکولهای هوا و لرزش خفیف محورهایشان ، با دامنههای خیلی کوچک نوسان میکنند. از اینرو انرژی نمیتواند تا صفر تنزل کند و در میانگین برابر kT باقی میماند. این حرکت را حرکت براونی گویند.
مدل عقربههای آهنربا و مفهوم صفر مطلق
در راستای ممکن اسپین در هر دما، احتمالهای متفاوت رخ میدهند. در دماهای خیلی پایین تقریبا همه الکترونها در تراز پایینتر جمع میشوند. یعنی اسپینهای آنها در راستای مخالف میدان قرار میگیرند. تراز بالاتر ، تقریبا تهی ، یعنی خالی از جمعیت میماند. هر چه دما بالاتر باشد، تراز بالاتر "پرجمعیت" میشود. به عنوان مثال در دماهای خیلی بالا (ε << KT) هر دو تصویر اسپین احتمال تقریبا برابر دارند. اگر دما پایین بیاید، بخش بزرگ و رو به افزایشی از اسپین الکترونها در راستای مخالف قرار میگیرند. اگر T = 0 باشد، اسپین همه الکترونها در راستای مخالف میدان قرار میگیرند. این حالت دستگاه با دمای صفر مطلق متناظر است.
مرکز انجمنهای تخصصی گنجینه دانش
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]

-
- پست: 5234
- تاریخ عضویت: پنجشنبه ۲۵ خرداد ۱۳۸۵, ۲:۴۷ ب.ظ
- سپاسهای ارسالی: 1747 بار
- سپاسهای دریافتی: 4179 بار
- تماس:
مفهوم صفر مطلق در نظریه کوانتومی
همانطور که در مباحث فوق عنوان شد، مفهوم صفر مطلق در نظریه کوانتومی معنای روشن و قاطعی دارد، در میان ترازهای انرژی هر دستگاه کوانتومی ترازی وجود دارد که با پایینترین انرژی متناظر است و در مثال ما ، این حالت حالتی است که اسپین همه الکترونها در راستای مخالف میدان قرار میگیرند. در صفر مطلق ، دستگاه در حالت پایه است، از اینرو نمیتواند به دستگاه دیگری انرژی انتقال دهد، دقیقا بدین سبب که تراز پایینتری وجود ندارد که بعد از ، از دست دادن انرژی به آن انتقال یابد.
دست نیافتنی بودن صفر مطلق
هر کسی میداند که دمای جسم را نمیتوان تا صفر مطلق پایین آورد، هر چند میتوان به آن نزدیک شد. برای اینکه دمای جسمی را تا صفر مطلق پایین بیاوریم لازم است مقداری متناهی گرما از آن بگیریم. برای اینکار از چرخه کارنو استفاده میکنیم:
T1/T2 = φ1/φ2
بدیهی است که در این نظر در چرخه کارنو مقدار گرما یا دما مطرح نیست، بلکه نسبت آنها مهم است. اکنون دیگر مشکل نیست که بفهمیم چرا برای پایین آوردن دمای جسمی تا صفر مطلق باید تعداد بی شماری مراحل را پشت سر گذاشت. هر مرحله میتواند یک چرخه بسته یا یک فرآیند تک ، مثل انبساط بی دررو گاز در حال سرد شدن باشد. در هر مرحله مقداری متناهی کار انجام میگیرید و دما به نسبت متناهی پایین میآید. از آنجا که هر مرحله مدت زمانی طول میکشد، زمان لازم برای پایین آوردن دمای جسم تا صفر مطلق لزوما نامتناهی است.
صفر مطلق و نظریه جنبشی گازها
میتوان پرسید که آیا دست نیافتنی بودن صفر مطلق در نظریه جنبشی گازها متفاوت است، آیا کسی میتواند اسپین همه الکترونها را به حالت پایه پایین بیاورد (به عنوان مثال ، آنقدر صبر کند که همه فزونی انرژیشان را تابش کنند. اما این سوال چیزی را روشن نمیکند. اگر دستگاه در یک فضای تهی نامتناهی بود و انرژیِ تابشی از آن برای همیشه دور میشود، اسپینها به یقین همه انرژیشان را از دست میدادند و دستگاه به حالتی متناظر با صفر مطلق میرسید. اما دستگاه در داخل حجمی باشد که دیوارههای آن در دمای ثابت نگه داشته میشود، آنگاه دستگاه دارای دمای دیوارهها میشود، در این صورت ممکن نیست بدون انجام دادن کار این دما را پایینتر آورد.
همانطور که در مباحث فوق عنوان شد، مفهوم صفر مطلق در نظریه کوانتومی معنای روشن و قاطعی دارد، در میان ترازهای انرژی هر دستگاه کوانتومی ترازی وجود دارد که با پایینترین انرژی متناظر است و در مثال ما ، این حالت حالتی است که اسپین همه الکترونها در راستای مخالف میدان قرار میگیرند. در صفر مطلق ، دستگاه در حالت پایه است، از اینرو نمیتواند به دستگاه دیگری انرژی انتقال دهد، دقیقا بدین سبب که تراز پایینتری وجود ندارد که بعد از ، از دست دادن انرژی به آن انتقال یابد.
دست نیافتنی بودن صفر مطلق
هر کسی میداند که دمای جسم را نمیتوان تا صفر مطلق پایین آورد، هر چند میتوان به آن نزدیک شد. برای اینکه دمای جسمی را تا صفر مطلق پایین بیاوریم لازم است مقداری متناهی گرما از آن بگیریم. برای اینکار از چرخه کارنو استفاده میکنیم:
T1/T2 = φ1/φ2
بدیهی است که در این نظر در چرخه کارنو مقدار گرما یا دما مطرح نیست، بلکه نسبت آنها مهم است. اکنون دیگر مشکل نیست که بفهمیم چرا برای پایین آوردن دمای جسمی تا صفر مطلق باید تعداد بی شماری مراحل را پشت سر گذاشت. هر مرحله میتواند یک چرخه بسته یا یک فرآیند تک ، مثل انبساط بی دررو گاز در حال سرد شدن باشد. در هر مرحله مقداری متناهی کار انجام میگیرید و دما به نسبت متناهی پایین میآید. از آنجا که هر مرحله مدت زمانی طول میکشد، زمان لازم برای پایین آوردن دمای جسم تا صفر مطلق لزوما نامتناهی است.
صفر مطلق و نظریه جنبشی گازها
میتوان پرسید که آیا دست نیافتنی بودن صفر مطلق در نظریه جنبشی گازها متفاوت است، آیا کسی میتواند اسپین همه الکترونها را به حالت پایه پایین بیاورد (به عنوان مثال ، آنقدر صبر کند که همه فزونی انرژیشان را تابش کنند. اما این سوال چیزی را روشن نمیکند. اگر دستگاه در یک فضای تهی نامتناهی بود و انرژیِ تابشی از آن برای همیشه دور میشود، اسپینها به یقین همه انرژیشان را از دست میدادند و دستگاه به حالتی متناظر با صفر مطلق میرسید. اما دستگاه در داخل حجمی باشد که دیوارههای آن در دمای ثابت نگه داشته میشود، آنگاه دستگاه دارای دمای دیوارهها میشود، در این صورت ممکن نیست بدون انجام دادن کار این دما را پایینتر آورد.
مرکز انجمنهای تخصصی گنجینه دانش
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]
[External Link Removed for Guests]
مرکز انجمنهای اعتقادی گنجینه الهی
[External Link Removed for Guests]